Design project: The top playground
Summary of task
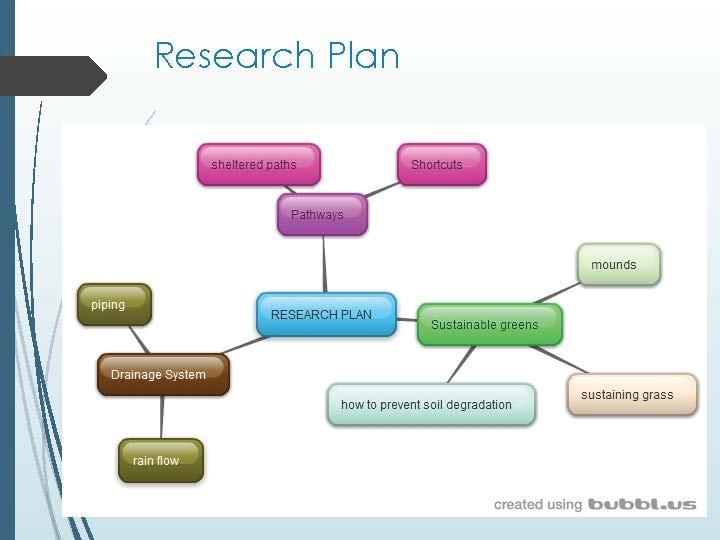
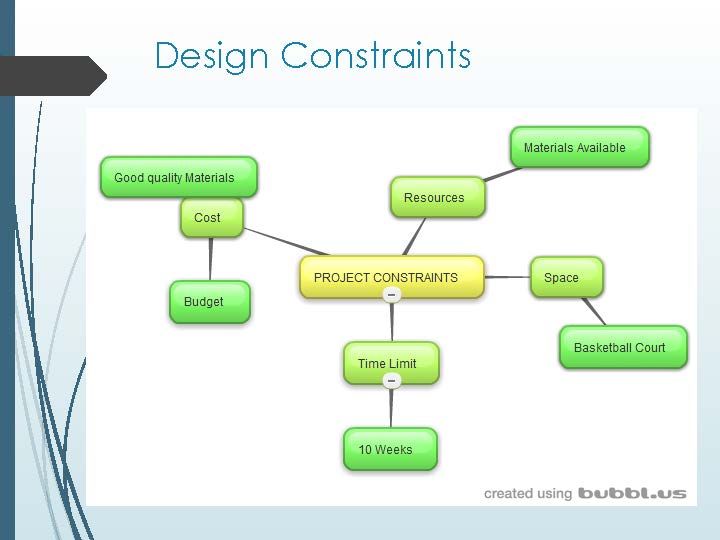
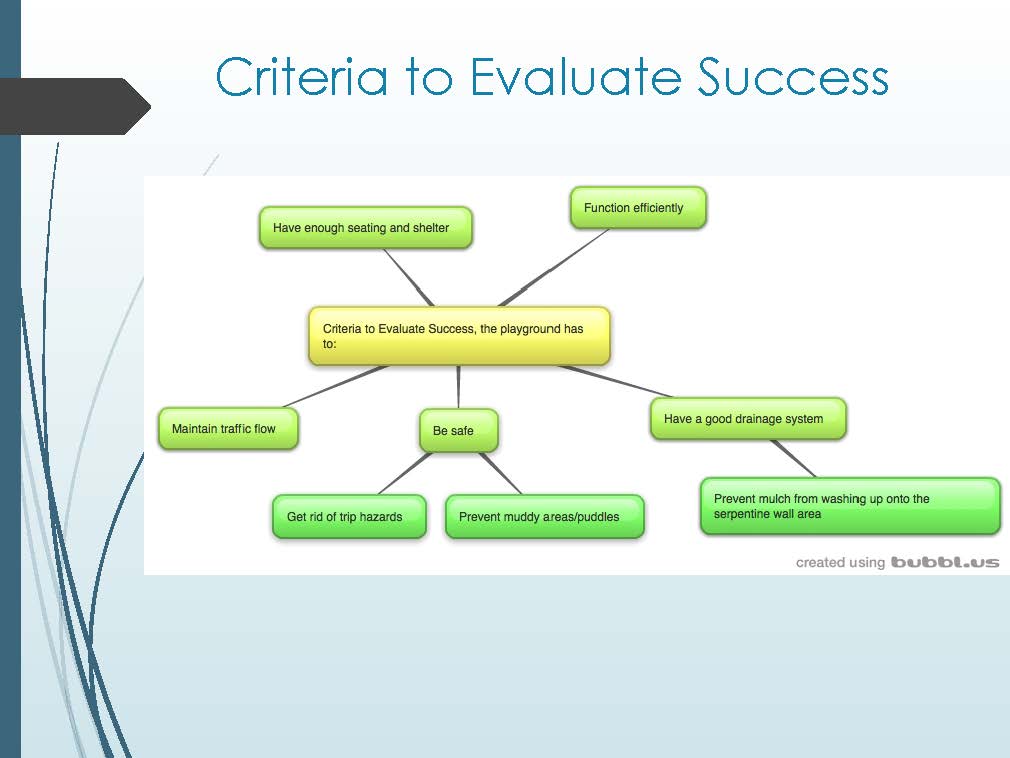
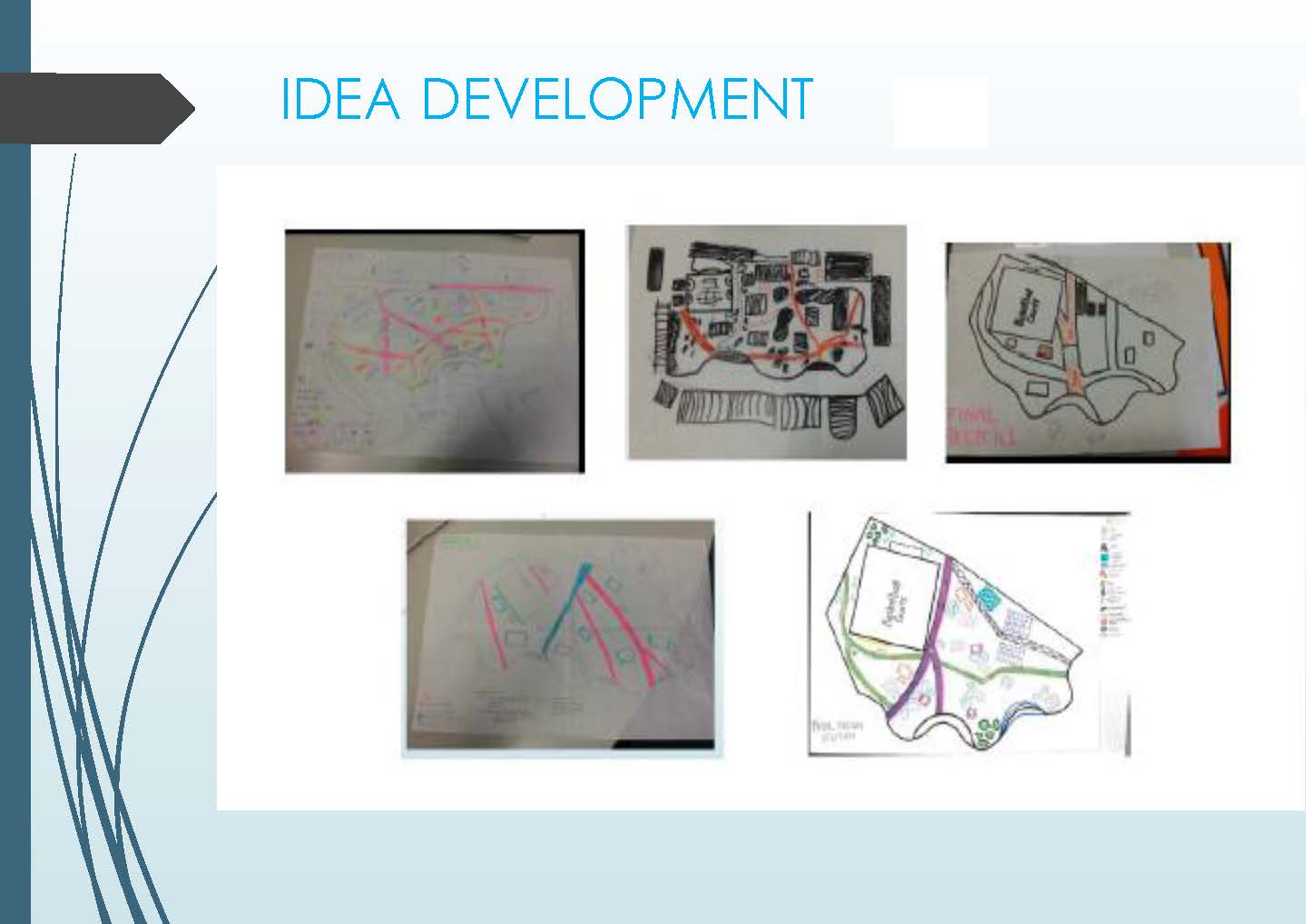
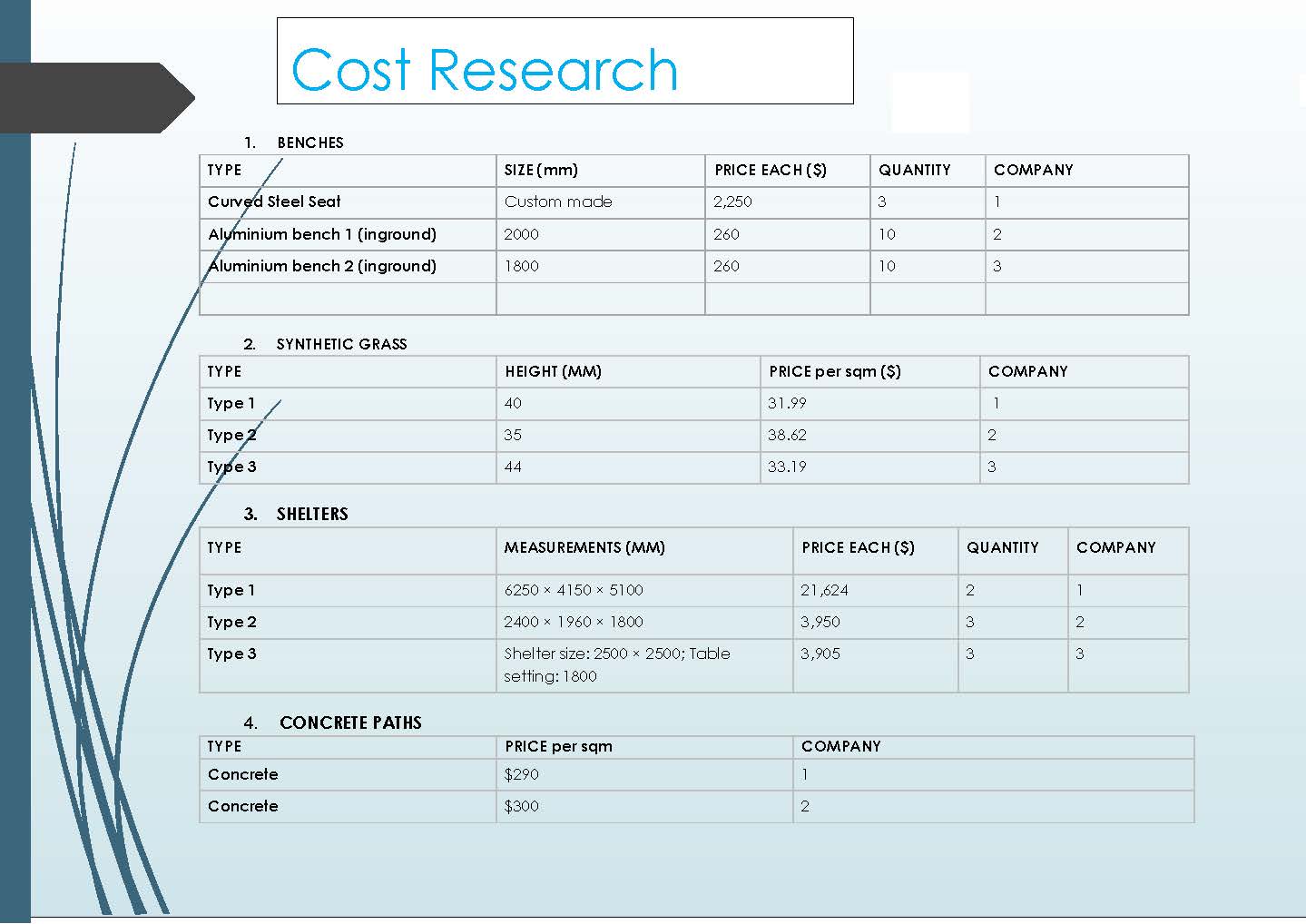
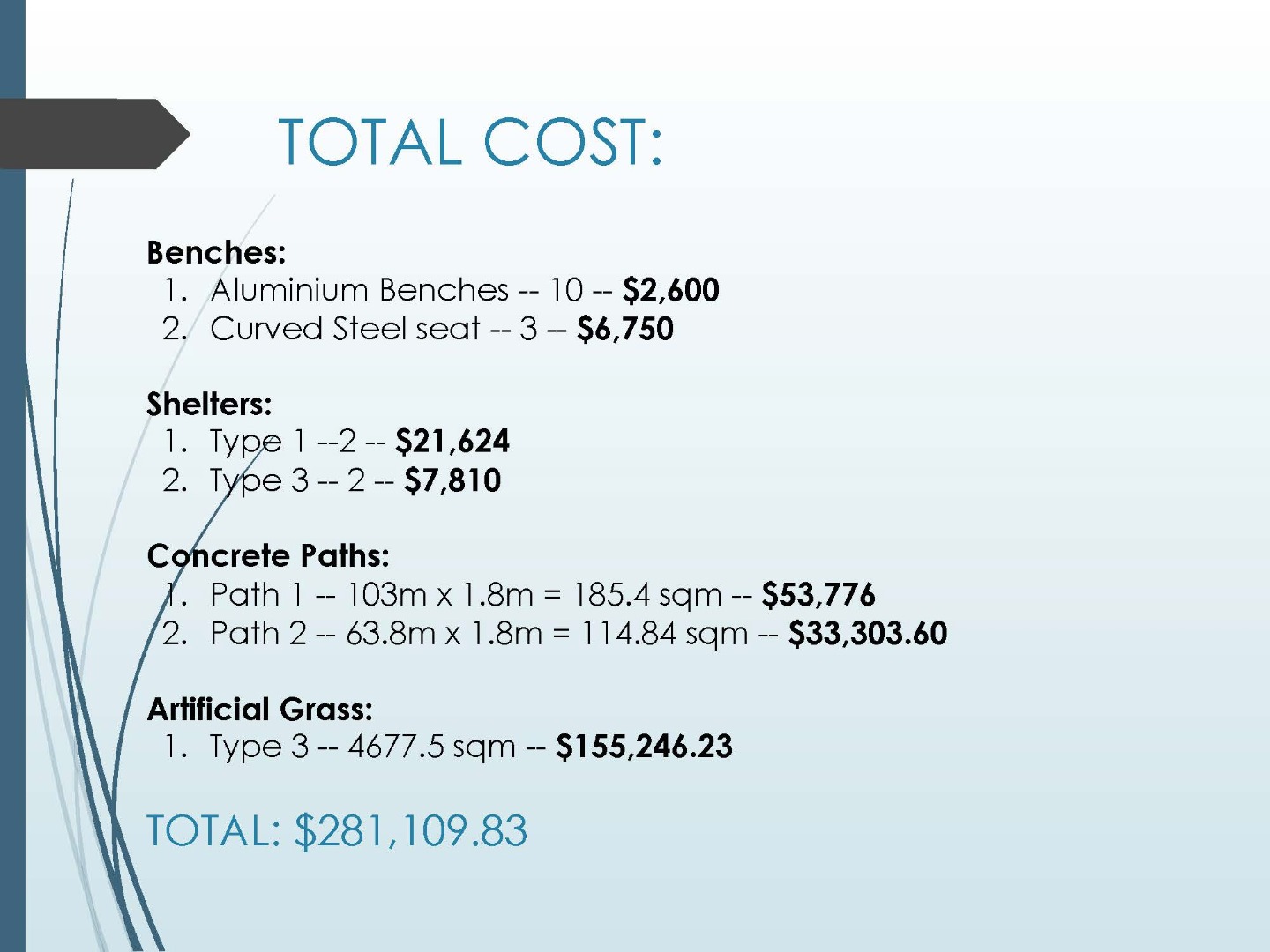
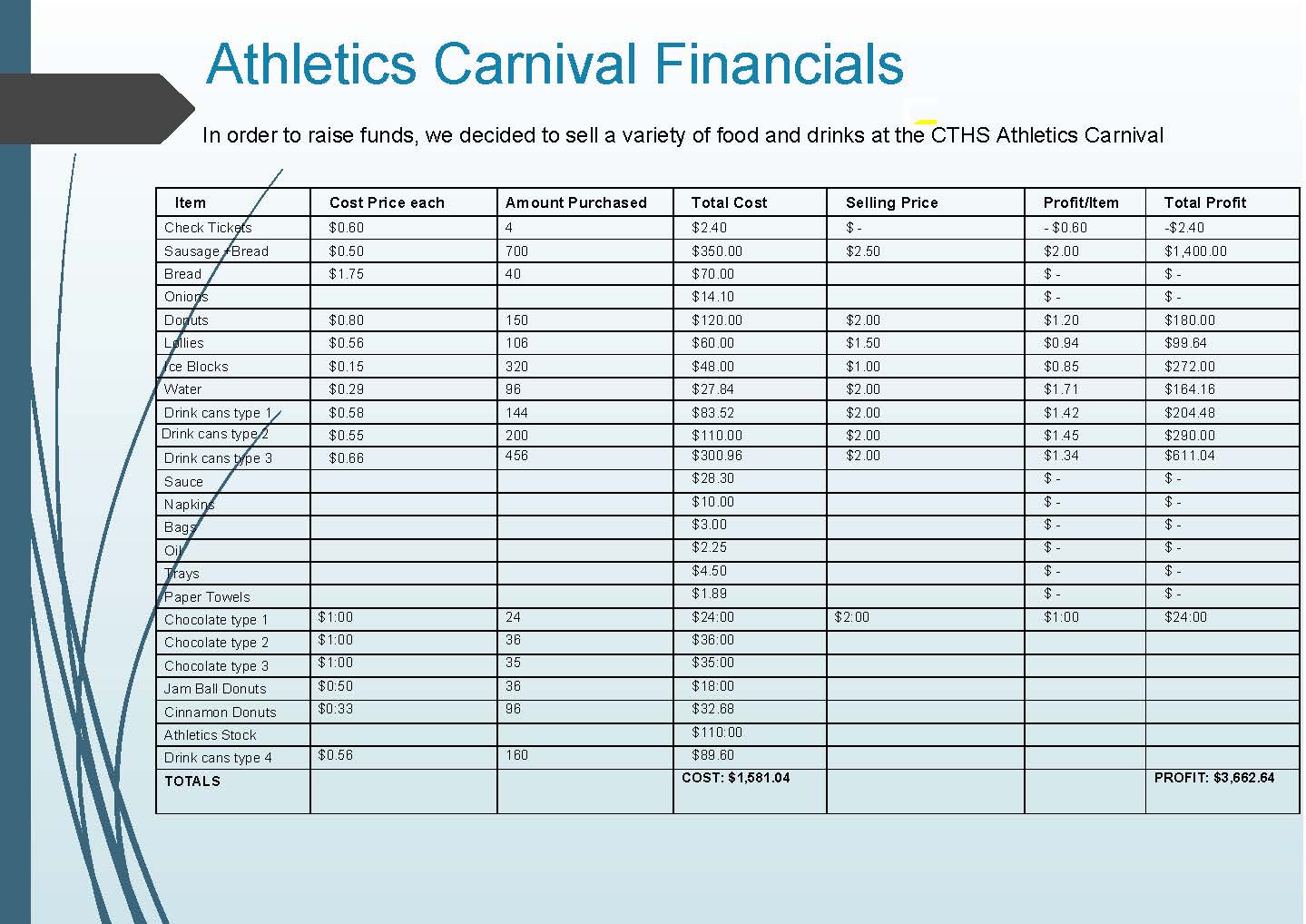
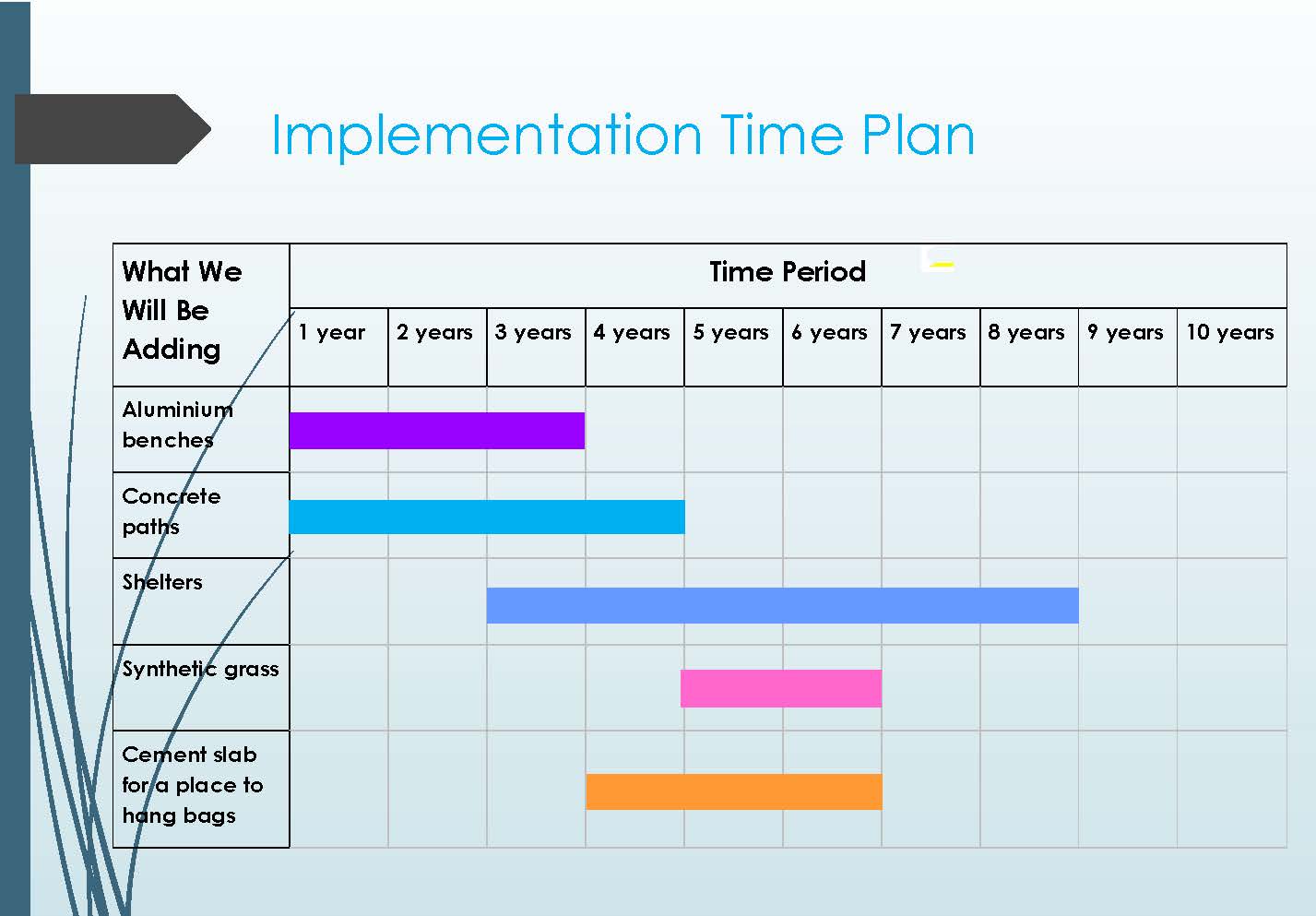
This task is the culmination of an extended unit of work that aimed to make connections for students between STEM disciplines in a project that targeted an identified need in the school. Students collaborated in small groups to investigate the effect of overpopulation on the school’s top playground. They were asked to design a potential solution to address the identified problems, using their knowledge of the design process and mathematical, technological and scientific tools.
Achievement Standards
Design and Technologies
By the end of Year 10, students explain how people working in design and technologies occupations consider factors that impact on design decisions and the technologies used to produce products, services and environments. They identify the changes necessary to designed solutions to realise preferred futures they have described. When producing designed solutions for identified needs or opportunities, students evaluate the features of technologies and their appropriateness for purpose for one or more of the technologies contexts.
Students create designed solutions for one or more of the technologies contexts based on a critical evaluation of needs or opportunities. They establish detailed criteria for success, including sustainability considerations, and use these to evaluate their ideas and designed solutions and processes. They create and connect design ideas and processes of increasing complexity and justify decisions. Students communicate and document projects, including marketing for a range of audiences. They independently and collaboratively apply sequenced production and management plans when producing designed solutions, making adjustments to plans when necessary. They select and use appropriate technologies skilfully and safely to produce high-quality designed solutions suitable for the intended purpose.
Digital Technologies
By the end of Year 10, students explain the control and management of networked digital systems and the security implications of the interaction between hardware, software and users. They explain simple data compression, and why content data are separated from presentation.
Students plan and manage digital projects using an iterative approach. They define and decompose complex problems in terms of functional and non-functional requirements. Students design and evaluate user experiences and algorithms. They design and implement modular programs, including an object-oriented program, using algorithms and data structures involving modular functions that reflect the relationships of real-world data and data entities. They take account of privacy and security requirements when selecting and validating data. Students test and predict results and implement digital solutions. They evaluate information systems and their solutions in terms of risk, sustainability and potential for innovation and enterprise. They share and collaborate online, establishing protocols for the use, transmission and maintenance of data and projects.
By the end of Year 9, students solve problems involving simple interest. They interpret ratio and scale factors in similar figures. Students explain similarity of triangles. They recognise the connections between similarity and the trigonometric ratios. Students compare techniques for collecting data from primary and secondary sources. They make sense of the position of the mean and median in skewed, symmetric and bi-modal displays to describe and interpret data.
Students apply the index laws to numbers and express numbers in scientific notation. They expand binomial expressions. They find the distance between two points on the Cartesian plane and the gradient and midpoint of a line segment. They sketch linear and non-linear relations. Students calculate areas of shapes and the volume and surface area of right prisms and cylinders. They use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles. Students calculate relative frequencies to estimate probabilities, list outcomes for two-step experiments and assign probabilities for those outcomes. They construct histograms and back-to-back stem-and-leaf plots.