Data is a general term for information (observations and/or measurements) collected during any type of systematic investigation.
A data display is a visual format for organising and summarising data. Examples include box plots, column graphs, frequency tables, scatter plots, and stem plots.
A decimal is a numeral in the decimal number system, which is the place-value system most commonly used for representing real numbers. In this system numbers are expressed as sequences of Arabic numerals 0 to 9, in which each successive digit to the left or right of the decimal point indicates a multiple of successive powers of 10; for example, the number represented by the decimal 123.45 is the sum
1×102+2×101+3×100+4×10−1+5×10−2
=1×100+2×10+3×1+4×110+5×1100
The digits after the decimal point can be terminating or non-terminating. A terminating decimal is a decimal that contains a finite number of digits, as shown in the example above. A decimal is non-terminating, if it has an infinite number of digits after the decimal point. Non-terminating decimals may be recurring, that is, contain a pattern of digits that repeats indefinitely after a certain number of places. For example, the fraction 13, written in the decimal number system, results in an infinite sequence of 3s after the decimal point. This can be represented by a dot above the recurring decimal.
13=0.333333⋯=0.˙3
Similarly, the fraction 17 results in a recurring group of digits, which is represented by a bar above the whole group of repeating digits
17=0.142857142857142857⋯=0.¯142857
Non-terminating decimals may also be non-recurring, that is the digits after the decimal point never repeat in a pattern. This is the case for irrational number, such as pi, e, or √2. For example,
π=3.1415926535897932384626433832795028841971693993751058209749…
Irrational numbers can only be approximated in the decimal number system.
In any fraction in the form ab , b is the denominator. It represents the number of equal parts into which the whole has been divided. For example, in the diagram below, a rectangle has been divided into 5 equal parts. Each of those parts is one fifth of the whole and corresponds to the unit fraction 15..

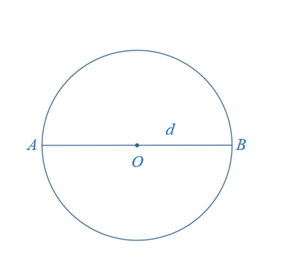
A diameter is a chord that passes through the centre of a circle. The word diameter is also used to refer to the length of the diameter. The diameter d of the circle below is represented by line segment AB.
A difference is the result of subtracting one number or algebraic quantity from another. For example, the difference between
Multiplication of numbers is said to be ‘distributive over addition’, because the product of one number with the sum of two others equals the sum of the products of the first number with each of the others. For example, the product of 3 with (4+5) gives the same result as the sum of 3×4 and 3×5:
3×(4+5)=3×9=27 and 3×4+3×5=12+15=27
This distributive law is expressed algebraically as follows:
a(b+c)=ab+ac, for all numbers a,b and c.
In general, a number or algebraic expression x is divisible by another y, if there exists a number or algebraic expression q of a specified type for which x=yq.
A natural number m is divisible by a natural number n if there is a natural number q such that m=nq; for example, 12 is divisible by 4 because 12=3×4.
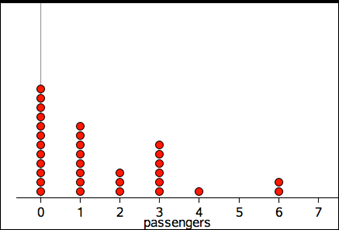
A dot plot is a graph used in statistics for organising and displaying categorical data or discrete numerical data.
The dot plot below displays the number of passengers observed in 32 cars stopped at a traffic light.