The leading term of a polynomial is the term that contains the variable raised to the highest power. For example, in the polynomial 3x2−5x+2, the leading term is 3x2.
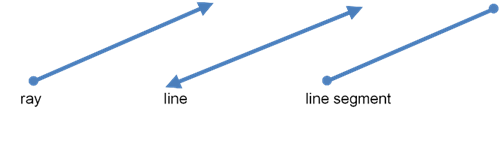
In geometry, a line extends infinitely in both directions.
A line is different from a ray (which extends from a point toward infinity) and a line segment (which extends between two points). Lines are depicted with arrow heads on both ends to distinguish them from rays and line segments.
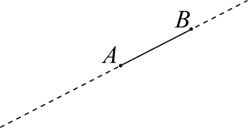
If A and B are two points on a line, the part of the line between and including A and B is called a line segment or interval.
The distance AB is a measure of the length of AB.
A linear equation is an equation involving just linear terms, that is, no variables are raised to a power greater than one. The general form of a linear equation in one variable is ax+b=0, where a and b cannot both be 0. The solution of a linear equation in general form is x=−ba
A linear equation with two variables takes the general form ax+by+c=0, where a and b cannot both be 0. If a≠0, then the point where the line intersects the x-axis (the x-intercept) is ca.
If b≠0, then the point where the line intersects the y-axis (the y-intercept) is cb.
Two-variable, or two-dimensional linear equations also come in the form y=mx+b. The constant m indicates the gradient or slope of a line, while b represents the y-intercept.
In Measurement and Geometry, the relative position of an object is referred to as its location. It can be expressed in terms of a description (such as ‘next to’, ‘behind’, ‘on top of’), a grid reference (such as ‘A5’), or a coordinate (such as ‘(-2,7)’).
In Statistics and Probability, a measure of location is a single number that can be used to indicate a central or ‘typical value’ within a set of data. The most commonly used measures of location are the mean and the median although the mode is also sometimes used for this purpose.
The logarithm of a positive number x is the power to which a given number b, called the base, must be raised in order to produce the number x. The logarithm of x, to the base b is denoted by logbx.
Algebraically, the statements logbx=y and by=x are equivalent in the sense that both statements express the identical relationship between x, y and b. For example, log10100=2 because 102=100,, and log2(132)=−5 because 2−5=132.