Mass is the measure of how much matter is in a person, object, or substance. Mass is measured in grams, kilograms, tonnes, ounces, or pounds. It is distinct from weight, which refers to the amount of gravitational force acting on matter. If you travelled to Mars, your mass would be the same as it was on Earth, but your weight would be less due to the weaker gravitational force on Mars.
The arithmetic mean of a list of numbers is the sum of the data values divided by the number of numbers in the list.
In everyday language, the arithmetic mean is commonly called the average; for example, for the following list of five numbers, {2, 3, 3, 6, 8}, the mean equals \(\frac{2+3+3+6+8}5=\frac{22}5=4.4\)
In statistics, the term measures of central tendency refers to different methods of calculating typical values (commonly called averages) within a set. The most commonly used measures of central tendency are the mean, median, and mode.
The median is the value in a set of ordered data that divides the data into two parts. It is frequently called the ‘middle value’.
Where the number of observations is odd, the median is the middle value; for example, for the following ordered data set with an odd number of observations, the median value is five.
1 3 3 4 5 6 8 9 9
Where the number of observations is even, the median is calculated as the mean of the two central values; for example, in the following ordered data set, the two central values are 5 and 6, and median value is the mean of these two values, 5.5.
1 3 3 4 5 6 8 9 9 10
The median provides a measure of location of a data set that is suitable for both symmetric and skewed distributions and is also relatively insensitive to outliers.
The midpoint M of a line segment AB, which extends between points A and B, is the point that divides the segment into two equal parts.
If \(A\;\left(x_1,\;y_1\right)\) and \(B\;(x_2,\;y_2)\) are points on a Cartesian plane, then the midpoint M of the line segment AB has coordinates \(\left(\frac{x_1+\;x_2}2,\;\;\frac{y_1+\;y_2}2\right)\)
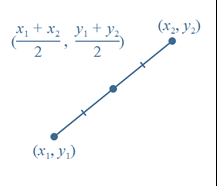
The mode is a measure calculated by identifying the value that appears with greatest frequency in a set of data. If two numbers occur in a set with equal frequency, the set is said to contain bimodal data. If there are more than two numbers in a set that occur with equal frequency, the set is said to contain multimodal data. The mode of the set {1, 2, 3, 4, 4, 5} is 4. In the set {1, 2, 2, 4, 5, 7, 7}, the modes are both 2 and 7, making the set bimodal. The mode is sometimes used as a measure of location.
A monic polynomial is one in which the coefficient of the leading term is 1.
For example, \(x^3+2x^2-7\) is monic, but \(4x^2-x+1\) is not.
Multimodal data is data whose distribution has more than two modes.
A multiple of a whole number is the product of that number and an integer.
A multiple of a real number \(x\) is any number that is a product of \(x\) and an integer; for example,
4.5 and -13.5 are multiples of 1.5 because 4.5=3×1.5 and -13.5=-9×1.5.