Numbers or algebraic expressions are factors (or divisors) of another number if they multiply to give that number. For example, 3 and 4 are factors of 12 as 3×4=12. This can be written algebraically as
x and y are factors of m, if m=xy
For polynomial expressions the same rule applies. For example, x−4 and x−2 are factors of the quadratic expression x2−6x+8 because (x−4)(x−2)=x2−6x+8.
According to the factor theorem, if p(x) is a polynomial and p(a)=0 for some number a, then x−a is a factor of p(x). Conversely, if p(x) is divisible by x−a then p(a)=0.
This follows from the more general remainder theorem, which states that the remainder of the division of a polynomial p(x) by a linear polynomial x−a is equal to p(a). This relationship is often stated in the form px=q(x)(x−a)+p(a), where q(x) is another polynomial, usually referred to as the quotient. It follows that, if p(a)=0, the remainder is 0 and p(x) is divisible by x−a.
The factor theorem can be used to obtain factors of a polynomial; for example, if p(x)=x3−3x2+5x−6, then it is easy to check that p(2)=23−3×22+5×2−6=0. So by the factor theorem x−2 is a factor of x3−3x2+5x−6.
To factorise a number or algebraic expression is to express it as a product; for example,
15 is factorised when expressed as a product: 15=3×5.
x2−3x+2 is factorised when written as a product: x2−3x+2=(x−1)(x−2)
A five-number summary is a method of summarising a data set using five statistics: the minimum value, the lower quartile, the median, the upper quartile and the maximum value. Box plots are a useful method of graphically depicting five-number summaries.
The fraction \(\frac ab\) (written alternatively as a/b), where a and b are integers unequal to zero. For example, 35 refers to 3 of 5 equal parts of the whole.
In the fraction \(\frac ab\) the number a is the numerator and the number b is the denominator.
Frequency, or observed frequency, is the number of times that a particular value occurs in a data set. For grouped data, it is the number of observations that lie in that group or class interval.
An expected frequency is the number of times that a particular event is expected to occur when a chance experiment is repeated a number of times. If the experiment is repeated n times, and on each of those times the probability that the event occurs is p, then the expected frequency of the event is np.
For example, suppose that a fair coin is tossed 5 times and the number of heads showing recorded. Then the expected frequency of ‘heads’ is 5/2. This example shows that the expected frequency is not necessarily an observed frequency, which in this case is any one of the numbers 0, 1, 2, 3, 4 or 5.
The relative frequency is given by the ratio fn, where f is the frequency of occurrence of a particular data value or group of data values in a data set and n is the number of data values in the data set.
A frequency distribution is the division of a set of observations into a number of classes, together with a listing of the number of observations (the frequency) in that class. Frequency distributions can be displayed in the form of a frequency table, a two-way-table or in graphical form.
A frequency table lists the frequency (number of occurrences) of observations in different ranges, called class intervals.
The frequency distribution of the heights (in cm) of a sample of 46 people is displayed in the form of a frequency table below.
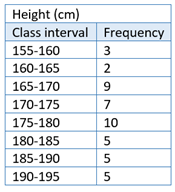
The information in a frequency table can also be displayed graphically in the form of a histogram or using a column graph.
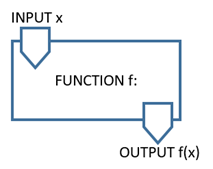
A function f assigns to each element of a set of input values (called the domain) precisely one element of a set of output values (called the range). In mathematical modelling, the independent variable is usually chosen as the input values for the function. The output values then represent the dependent variable.
Functions are usually defined by a formula for f(x) in terms of x; for example, the formula f(x)=x2 defines the ‘squaring function’ that maps each real number x to its square x2. The graph of this function is shown below.